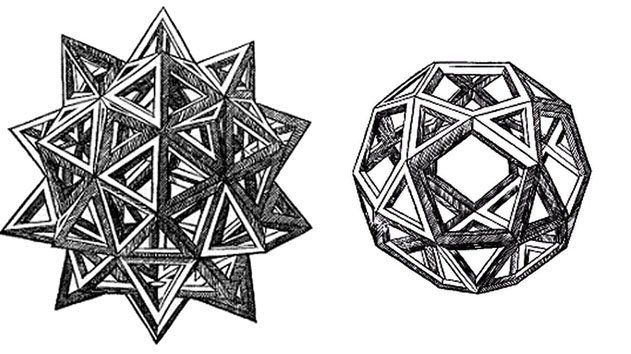
Divina Proportione
Polyhedra interpretation
Reinterpretación artística del estudio de los poliedros a lo largo de la historia.
He elegido algunos de los poliedros para proyectar mi obra artística realizada en Porcelana, lustre de Oro y Platino.
Production stages, technique:: Slipcasting of Porcelain. Plaster cast of pyramids´s moulds, pouring of Porcelain , Glaze with second glaze-firing at a temperature of about 1,300 °C (2,370 °F) and a Bright Gold & Platinum´s lustre technic with a third firing 800 °C (1,472 °F) and a Lithography or transfer print with a fourth firing 750 °C (1,282 °F).
Todas las obras las he generado a través de ELEVAR, HUNDIR y ESTELAR algunas de las caras de los poliedros, igual que hacía Leonardo de Vinci en sus dibujos.
La estética de las obras es muy barroca, creando y dibujando mundos soñados como Escher sobre los poliedros, para crear diferentes visiones espaciales dentro de una misma obra que ya de por si son figuras geométricas puras.
Cada obra lleva el nombre del poliedro que lo engendra, y que lleva en su interior como si de un alma se tratara.
Para la producción de las obras, se ha realizado moldes de escayola, para el vaciado de la porcelana, y cada obra lleva 3 o 4 cocciones:
El bizcochado a 900 ºC, el esmaltado brillo transparente a 1220 ºC, la serigrafía a 750 ºC y el lustre de Oro o Platino a 700 ºC.
La cerámica está muy unida al mundo de los poliedros: Platón representaba el Fuego, la tierra, el agua, el aire y el Universo con un Tetraedro, un cubo, un icosaedro , un Octaedro y un Dodecaedro respectivamente.
Los poliedros se encontraron en el Neólitico en Escocia, estudiados por primera vez por Arquímedes en la antigua Grecia, asociados a la Naturaleza por Empédocles, y relacionados a las estrellas por Platón, inscritos en una esfera por Euclides de Alejandría, clasificados por Arquímedes, transformados por Catalan, estrellados por Kepler-Poinsot, incorporados a las pinturas de Paolo Uccello ó Piero della Francesca ó Durero y publicados en la De divina proportione de 1509 por Luca Bartolomeo Pacioli buscando la proporción áurea y su aplicación a la arquitectura, con la incorporación de dibujos sobre los sólidos platónicos de Leonardo da Vinci, y llegando a la creatividad del orfebre Wentzel Jamnitzer y los dibujos de Maurits Cornelis Escher.
Esta reinterpretación artística de los poliedros es un paso más en este juego infinito del mundo de los poliedros.
Mac Fine Art Gallery833 NE 4th Avenue. Fort Lauderdale. USA
.